Exploring Tetration: The Enormous Numbers Beyond Everyday Math

Mathematics is vast and filled with concepts that often remain untouched outside academic circles. One such concept is tetration, a mathematical operation involving repeated exponentiation, creating unimaginably large numbers. In this article, we delve into tetration, understand its significance (or lack thereof in everyday life), and clarify how it differs from traditional mathematical operations such as addition, multiplication, and exponentiation. If you’ve never seen a number like the ones discussed here—you’re not alone. Let’s explore this fascinating realm of large numbers together.

Introduction to tetration and its rarity

Tetration: Entering the world of colossal numbers

The video begins by stating that most people on Earth will never encounter numbers of this magnitude in their lives—let alone use them. Why? Because tetration produces numbers that are so immense they defy comprehension. Numbers resulting from tetration are "bigger than what you can imagine" because even when expressed with small bases, their scale far surpasses typical numerical concepts.

Unlike addition or multiplication, which we commonly use in daily tasks, or exponentiation, which appears in scientific and financial calculations, tetration operations escalate into scales that hold minimal relevance to practical applications.

What is tetration?

Tetration, denoted as ( ^n a ), is essentially an iterated exponentiation operation. To understand this, let us begin with some basic operations for comparison:

Addition: Repeatedly adding a number, such as (3 + 3 + 3), gives (9).
Multiplication: Repeated addition, such as (3 \times 3 = 9).
Exponentiation: Repeated multiplication, such as (3^3 = 27).

Tetration, however, takes this one step further. For example, ( ^3 10 ) means (10^{10^{10}})—a number so large that it escapes expression in typical numerical formats.

In the video, the speaker begins by showing a simple way to understand exponentiation before diving into tetration.

Exponentiation explained: The building block

Understanding exponentiation as the foundation of tetration

Starting with exponentiation, the speaker emphasizes its simplicity through familiar examples:

Consider (10^2): This is equivalent to (10 \times 10 = 100). The exponent (“2”) specifies the number of times you multiply the base ((10)) by itself.
As you increase the exponent, the resulting number grows exponentially. For instance, (10^3 = 1,000), an increase of almost 900 compared to (10^2).

The effect of incrementing the exponent even slightly is described as “huge,” especially when the base number is large. This rapid growth is central to understanding how quickly numbers spiral out of control during tetration.

The magnitude of exponentiation

An increase in the exponent, even by 1, leads to drastic numerical growth

The presenter uses relatable analogies to illustrate just how significant the numerical growth can become:

Imagine your monthly salary suddenly increasing from $100 to $11,000—this is the effect of adding a single digit to the exponent. The gap between such numbers is truly astronomical, representing the powerful amplification effect of exponentiation.

For example:

(10^4 = 10,000), which is a 9,000-unit increase from (10^3 = 1,000).
When the exponent increases with a reasonably large base, the difference between results compounds more severely than with addition or multiplication.

Introducing tetration

Moving beyond basic exponentiation, the speaker introduces tetration and uses this to highlight its astronomical growth compared to simple exponentiation.

Visualizing tetration: Using exponentiation as a springboard to this concept

In one example, we explore the third tetration of 10. Written as ( ^3 10 ), this expands to (10^{10^{10}}). Here’s the breakdown:

(10^3 = 1,000), which involves multiplying (10 \times 10 \times 10).
Now imagine that ( ^3 10 = 10^{(10^{10})})—meaning you stack these exponents. This is far beyond merely three zeros; it involves one followed by 10 billion zeros!

Such a number is incomprehensible for humans to write or visualize, let alone use in practical applications. Effectively, tetration scales numbers to realms where even writing them physically becomes impossible.

Why tetration numbers are larger than the universe

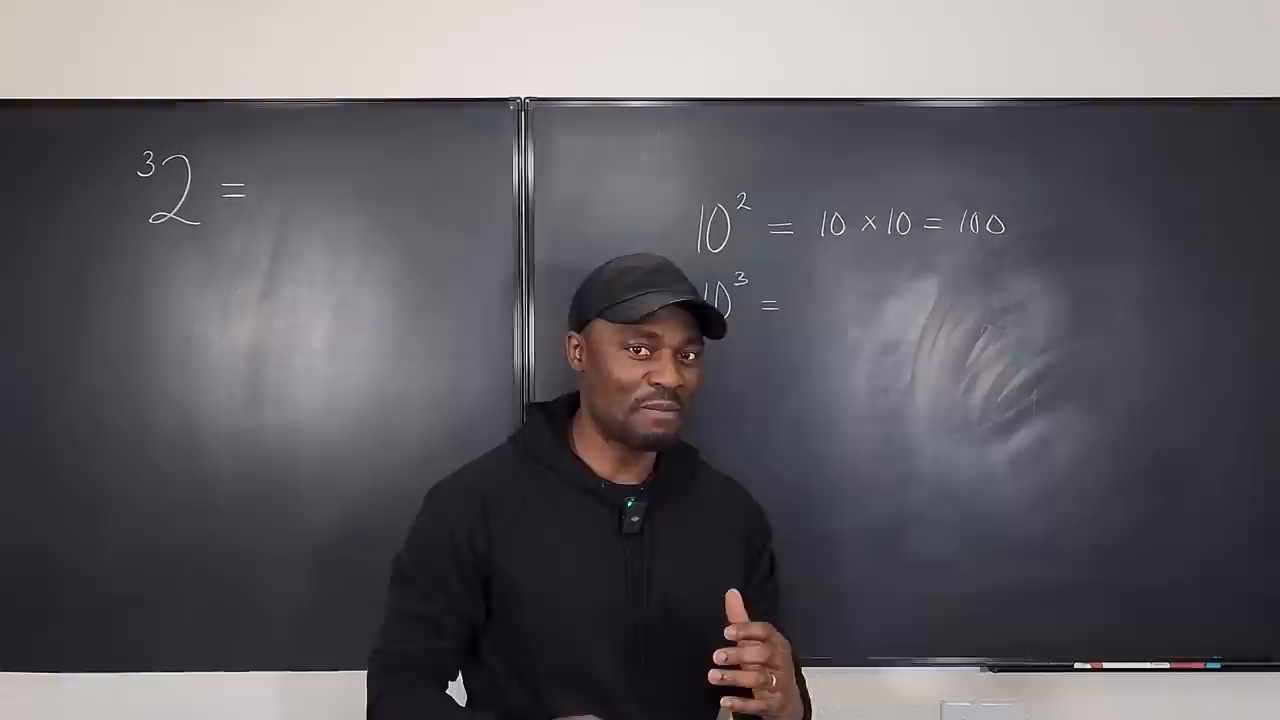
Tetration produces numbers larger than the total atoms in the universe

The presenter explains that (10^{10^{10}}) results in a number so large that it surpasses cosmic scales. A single calculation with tetration produces a value larger than the total number of atoms in the observable universe!

This example emphasizes why tetration is of little use in everyday mathematics. The numbers grow so quickly that they exceed the boundaries of human comprehension, storage, and application. Beyond their theoretical interest, they remain untethered to practical scenarios.

Translating tetration to exponential notation

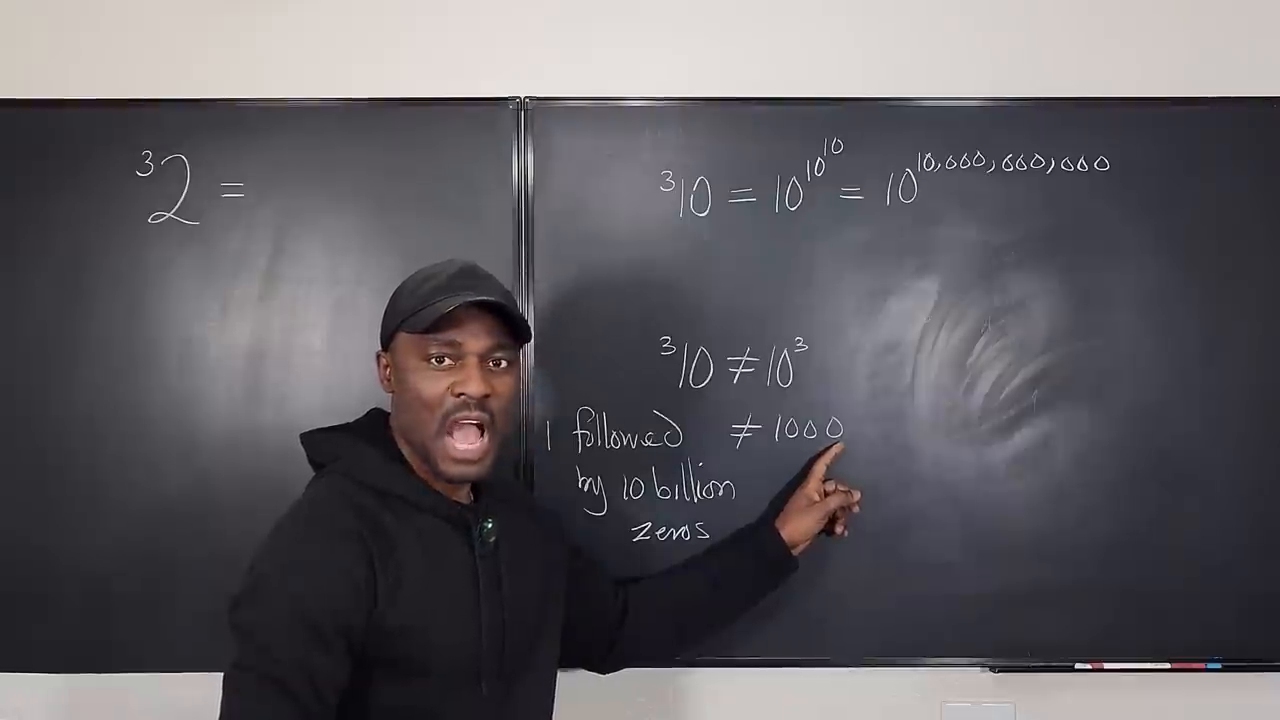
Converting tetration into an expressible exponential format

The process of breaking down tetration back into exponentiation is introduced as a way to understand how the operation functions. For example:

( ^3 10 ) can be written as (10^{10^{10}}).
Expanding this would involve stacking 10 billion and iterating repeated multiplication on top of itself.

Yet, a key takeaway here is that tetration bypasses realistic applications. Even expressing these numbers mathematically is computationally exhausting, let alone applying them.

Why tetration isn’t widely taught

The presenter humorously addresses why concepts like tetration aren’t studied extensively. The main reasons include:

Impracticality for everyday numbers: They grow so fast that they escape relevance for numerical or scientific calculations.
Educational limitations: Beyond a certain point, the behavior of such numbers exceeds what schools aim to teach.
Impossibility in representation: It’s literally impossible to write even a fraction of the zeros produced by tetration without exceeding human lifespans.

Conclusion: Understanding, not using, tetration

Tetration is a mind-bending concept that magnifies numbers into unimaginable territory. Despite its fascinating properties and mathematical elegance, its real-world applications are practically nonexistent. The video’s presenter challenges viewers to think critically about these colossal numbers and encourages them to explore more, reminding us: “Those who stopped learning have stopped living.”

While tetration might not find its way into your daily calculations, it offers a glimpse into the immense diversity and creativity present within mathematics—a subject that is truly boundless, much like the numbers tetration generates.

[Buy the T-shirt with the concept of tetration here: shorturl.at/HNUX1]