Explorando tetración: los enormes números más allá de las matemáticas cotidianas
Las matemáticas son vastas y están llenas de conceptos que a menudo permanecen sin tocarse fuera de los círculos académicos. Uno de estos conceptos es tetración, una operación matemática que involucra la exponenciación repetida, creando números inimaginablemente grandes. En este artículo, nos adentramos en la tetración, entendemos su importancia (o su falta en la vida cotidiana) y aclaramos cómo se diferencia de las operaciones matemáticas tradicionales como la adición, la multiplicación y la exponenciación. Si nunca has visto un número como los que se discuten aquí—no estás solo. Exploremos juntos este fascinante reino de grandes números.
Introducción a la tetración y su rareza

Tetración: ingresando al mundo de los números colosales
El video comienza afirmando que la mayoría de las personas en la Tierra nunca encontrarán números de esta magnitud en sus vidas—y mucho menos los usarán. ¿Por qué? Porque la tetración produce números que son tan inmensos que desafían la comprensión. Los números resultantes de la tetración son "más grandes de lo que puedes imaginar" porque incluso al expresarse con bases pequeñas, su escala supera con creces los conceptos numéricos típicos.
A diferencia de la suma o la multiplicación, que usamos comúnmente en tareas diarias, o la exponenciación, que aparece en cálculos científicos y financieros, las operaciones de tetración se elevan a escalas que tienen una relevancia mínima para aplicaciones prácticas.
¿Qué es la tetración?
La tetración, denotada como ( ^n a ), es esencialmente una operación de exponenciación iterada. Para entender esto, comencemos con algunas operaciones básicas para comparación:
- Adición: Sumar repetidamente un número, como (3 + 3 + 3), da (9).
- Multiplicación: Adición repetida, como (3 \times 3 = 9).
- Exponenciación: Multiplicación repetida, como (3^3 = 27).
La tetración, sin embargo, lleva esto un paso más allá. Por ejemplo, ( ^3 10 ) significa (10^{10^{10}})—un número tan grande que escapa a la expresión en formatos numéricos típicos.
En el video, el presentador comienza mostrando una manera simple de entender la exponenciación antes de profundizar en la tetración.
Exponenciación explicada: el bloque de construcción

Entendiendo la exponenciación como la base de la tetración
Comenzando con exponenciación, el presentador enfatiza su simplicidad a través de ejemplos familiares:
- Considera (10^2): Esto es equivalente a (10 \times 10 = 100). El exponente (“2”) especifica el número de veces que multiplicas la base ((10)) por sí misma.
- A medida que aumentas el exponente, el número resultante crece exponencialmente. Por ejemplo, (10^3 = 1,000), un aumento de casi 900 en comparación con (10^2).
El efecto de incrementar el exponente incluso ligeramente se describe como “enorme,” especialmente cuando el número base es grande. Este crecimiento rápido es central para entender qué tan rápidamente los números se descontrolan durante la tetración.
La magnitud de la exponenciación

Un aumento en el exponente, incluso por 1, conduce a un crecimiento numérico drástico
El presentador utiliza analogías comprensibles para ilustrar cuán significativo puede llegar a ser el crecimiento numérico:
- Imagina que tu salario mensual aumenta de $100 a $11,000—este es el efecto de añadir un solo dígito al exponente. La diferencia entre tales números es verdaderamente astronómica, representando el poderoso efecto de amplificación de la exponenciación.
Por ejemplo:
- (10^4 = 10,000), que es un aumento de 9,000 unidades desde (10^3 = 1,000).
- Cuando el exponente aumenta con una base razonablemente grande, la diferencia entre resultados se compone más severamente que con la adición o la multiplicación.
Introduciendo la tetración
Pasando más allá de la exponenciación básica, el presentador introduce tetración y usa esto para resaltar su crecimiento astronómico en comparación con la exponenciación simple.

Visualizando la tetración: usando la exponenciación como trampolín para este concepto
En un ejemplo, exploramos la tercera tetración de 10. Escrito como ( ^3 10 ), esto se expande a (10^{10^{10}}). Aquí está el desglose:
- (10^3 = 1,000), lo que implica multiplicar (10 \times 10 \times 10).
- Ahora imagina que ( ^3 10 = 10^{(10^{10})})—lo que significa que apilas estos exponentes. Esto está muy por encima de simplemente tres ceros; implica uno seguido de 10 mil millones de ceros!
Tal número es incomprensible para que los humanos lo escriban o visualicen, y mucho menos para usarlo en aplicaciones prácticas. Efectivamente, la tetración escala los números a reinos donde incluso escribirlos físicamente se vuelve imposible.
Por qué los números de tetración son más grandes que el universo
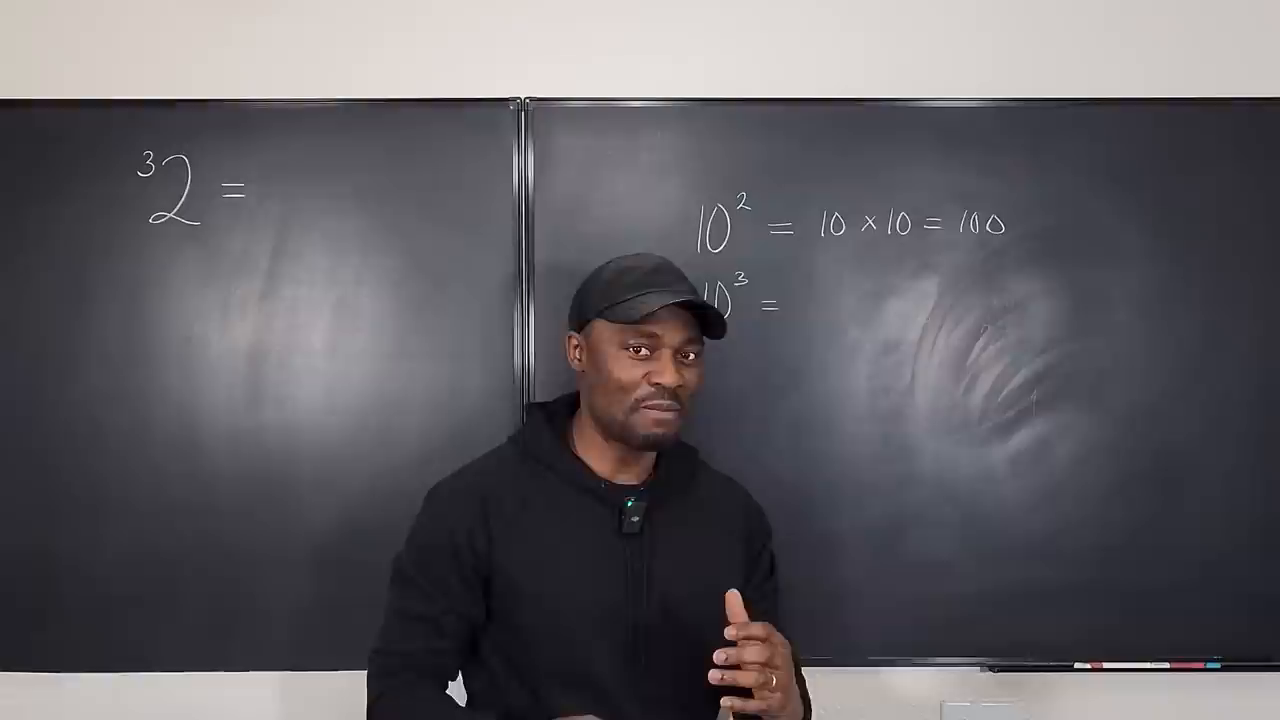
La tetración produce números más grandes que el total de átomos en el universo
El presentador explica que (10^{10^{10}}) resulta en un número tan grande que supera las escales cósmicas. Un solo cálculo con tetración produce un valor más grande que el número total de átomos en el universo observable!
Este ejemplo enfatiza por qué la tetración tiene poca utilidad en matemáticas cotidianas. Los números crecen tan rápidamente que superan los límites de la comprensión humana, el almacenamiento y la aplicación. Más allá de su interés teórico, permanecen desvinculados de escenarios prácticos.
Traduciendo tetración a notación exponencial
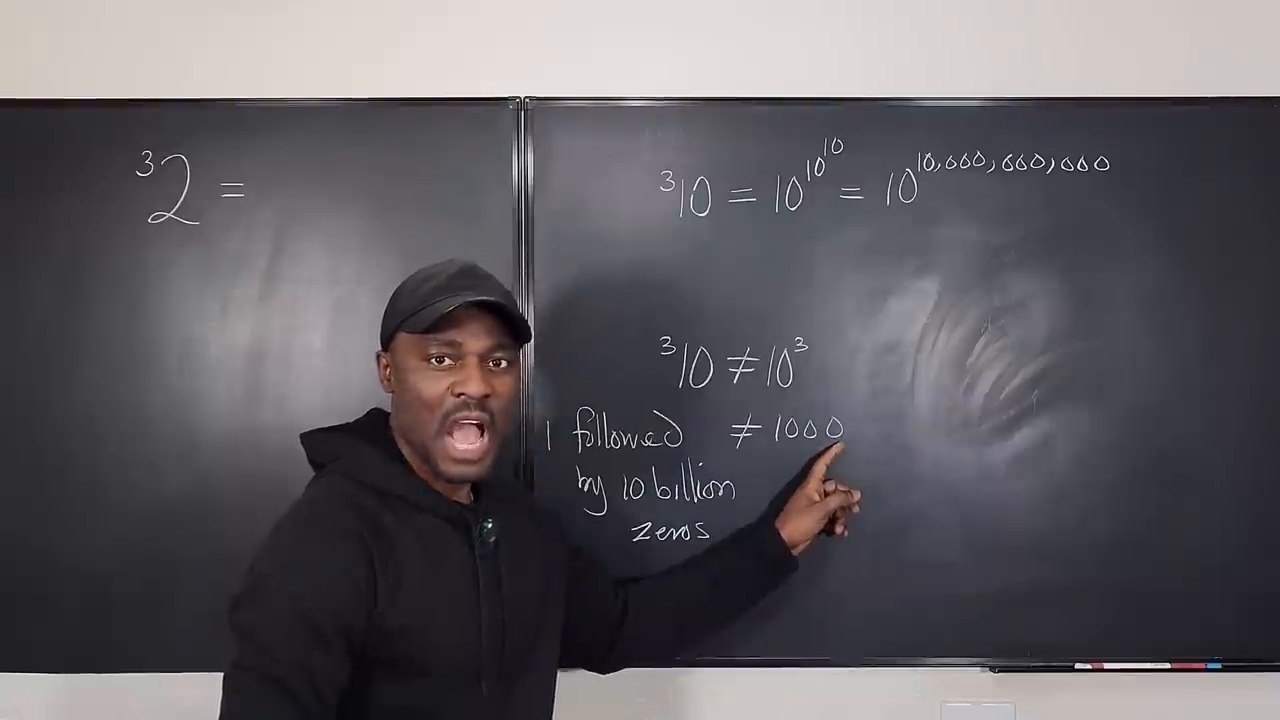
Convirtiendo la tetración en un formato exponencial expresable
El proceso de descomponer la tetración de nuevo en exponenciación se presenta como una manera de entender cómo funciona la operación. Por ejemplo:
- ( ^3 10 ) puede escribirse como (10^{10^{10}}).
- Expandir esto implicaría apilar 10 mil millones e iterar la multiplicación repetida sobre sí misma.
Sin embargo, una conclusión clave aquí es que la tetración evade aplicaciones realistas. Incluso expresar estos números matemáticamente es exhaustivo computacionalmente, y mucho menos aplicarlos.
Por qué la tetración no se enseña ampliamente
El presentador aborda humorísticamente por qué conceptos como la tetración no se estudian extensamente. Las principales razones incluyen:
- Impracticidad para números cotidianos: Crecen tan rápido que escapan a la relevancia para cálculos numéricos o científicos.
- Limitaciones educativas: Más allá de cierto punto, el comportamiento de tales números excede lo que las escuelas pretenden enseñar.
- Imposibilidad en la representación: Es literalmente imposible escribir incluso una fracción de los ceros producidos por la tetración sin exceder la duración de la vida humana.
Conclusión: entendiendo, no usando, la tetración
La tetración es un concepto que desafía la mente y magnifica los números a territorios inimaginables. A pesar de sus propiedades fascinantes y elegancia matemática, sus aplicaciones en el mundo real son prácticamente inexistentes. El presentador del video desafía a los espectadores a pensar críticamente sobre estos números colosales y los anima a explorar más, recordándonos: “Aquellos que dejaron de aprender han dejado de vivir.”
Mientras que la tetración puede no encontrar su camino en tus cálculos diarios, ofrece un vistazo a la inmensa diversidad y creatividad presente en las matemáticas—un tema que es verdaderamente ilimitado, al igual que los números que genera la tetración.
[Compra la camiseta con el concepto de tetración aquí: shorturl.at/HNUX1]
