Exploring tetration: The enormous numbers beyond everyday math

गणित विशाल है और ऐसे सिद्धांतों से भरा है जो अक्सर शैक्षणिक चक्रों के बाहर अनछुए रहते हैं। ऐसा ही एक सिद्धांत है टेट्रेशन, एक गणितीय क्रिया जो दोहराए गए घातांक के उपयोग से अविश्वसनीय रूप से बड़े संख्याएँ उत्पन्न करती है। इस लेख में, हम टेट्रेशन की खोज करेंगे, उसके महत्व को समझेंगे (या दैनिक जीवन में इसकी कमी) और यह परिभाषित करेंगे कि यह पारंपरिक गणितीय कार्यों जैसे जोड़, गुणा और घातांक से कैसे भिन्न है। अगर आपने कभी उन संख्याओं को नहीं देखा है जिनके बारे में यहाँ चर्चा की गई है—आप अकेले नहीं हैं। चलिए इस बड़े संख्याओं की आकर्षक दुनिया का अन्वेषण करते हैं।

Introduction to tetration and its rarity

Tetration: Entering the world of colossal numbers

वीडियो की शुरुआत इस बात से होती है कि धरती पर अधिकांश लोग कभी इस स्तर की संख्याओं का सामना नहीं करेंगे—यहाँ तक कि उनका उपयोग भी नहीं करेंगे। क्यों? क्योंकि टेट्रेशन इतने विशाल संख्याएँ उत्पन्न करता है कि वे समझ से परे हैं। टेट्रेशन से उत्पन्न संख्याएँ "आपकी कल्पना से बड़ी" होती हैं क्योंकि जब भी इन्हें छोटे आधारों के साथ व्यक्त किया जाता है, तब भी उनका पैमाना सामान्य संख्यात्मक अवधारणाओं को बहुत पार कर जाता है।

जोड़ या गुणा की तरह, जिसका हम दैनिक कार्यों में उपयोग करते हैं, या घातांक जो वैज्ञानिक और वित्तीय गणनाओं में दिखाई देता है, टेट्रेशन आंदोलनों में ऐसे पैमाने पर पहुँचता है जिसका व्यावहारिक अनुप्रयोगों से बहुत कम संबंध होता है।

What is tetration?

टेट्रेशन, जो ( ^n a ) के रूप में प्रदर्शित होता है, मूलतः एक पुनरावृत्त घातांक क्रिया है। इसे समझने के लिए, आइए कुछ मूलभूत कार्यों की तुलना करें:

1. जोड़: किसी संख्या का बार-बार जोड़ना, जैसे (3 + 3 + 3), हमें (9) देता है।
2. गुणा: पुनरावृत्त जोड़, जैसे (3 \times 3 = 9)।
3. घातांक: पुनरावृत्त गुणा, जैसे (3^3 = 27)।

टेट्रेशन, हालांकि, इसे एक कदम आगे ले जाता है। उदाहरण के लिए, ( ^3 10 ) का अर्थ है (10^{10^{10}})—एक संख्या इतनी बड़ी है कि इसे सामान्य संख्यात्मक प्रारूपों में व्यक्त करना असंभव है।

वीडियो में, वक्ता घातांक को समझाने के लिए एक सरल तरीका दिखाते हैं, फिर टेट्रेशन में गोता लगाते हैं।

Exponentiation explained: The building block

Understanding exponentiation as the foundation of tetration

घातांक से शुरू करते हुए, वक्ता इसके सरलता पर जोर देते हैं सरल उदाहरणों के माध्यम से:

• (10^2) पर विचार करें: यह (10 \times 10 = 100) के बराबर है। घातांक (“2”) यह निर्धारित करता है कि आप आधार ((10)) को कितनी बार स्वयं से गुणा करते हैं।
• जैसे-जैसे आप घातांक बढ़ाते हैं, परिणामस्वरूप संख्या तेजी से बढ़ती है। उदाहरण के लिए, (10^3 = 1,000), जो (10^2) की तुलना में लगभग 900 की वृद्धि है।

घातांक को थोड़े से बढ़ाने का प्रभाव "विशाल" के रूप में वर्णित है, विशेषकर जब आधार संख्या बड़ी हो। यह तेजी से वृद्धि इस बात के लिए केंद्रीय है कि कैसे टेट्रेशन के दौरान संख्याएँ नियंत्रण से बाहर निकलती हैं।

The magnitude of exponentiation

An increase in the exponent, even by 1, leads to drastic numerical growth

प्रस्तुतकर्ता संख्यात्मक वृद्धि के प्रभाव को स्पष्ट करने के लिए संबंधित उपमा का उपयोग करते हैं:

• تصور करें कि आपकी मासिक तनख्वाह अचानक $100 से $11,000 हो जाती है—यह ग्राफ के घातांक में एक अंक जोड़ने का प्रभाव है। ऐसी संख्याओं के बीच का अंतर वास्तव में अंतरिक्षीय है, जो घातांक के शक्तिशाली बढ़ाने के प्रभाव का प्रतिनिधित्व करता है।

उदाहरण के लिए:

• (10^4 = 10,000), जो (10^3 = 1,000) से 9,000 की वृद्धि है।
• जब घातांक एक उचित बड़े आधार के साथ बढ़ता है, तो परिणामों के बीच का अंतर जोड़ने या गुणा करने की तुलना में और भी गंभीरता से जोड़ता है।

Introducing tetration

बुनियादी घातांक से परे बढ़ते हुए, वक्ता टेट्रेशन का परिचय देते हैं और इस बात पर जोर देते हैं कि इसका वृद्धि घातांक की साधारण वृद्धि की तुलना में कितनी विशाल है।

Visualizing tetration: Using exponentiation as a springboard to this concept

एक उदाहरण में, हम 10 का तीसरा टेट्रेशन देखते हैं। इसे ( ^3 10 ) के रूप में लिखा जाता है, जो (10^{10^{10}}) में विस्तारित होता है। यहाँ विवरण है:

• (10^3 = 1,000), जिसमें (10 \times 10 \times 10) की गुणा शामिल है।
• अब सोचें कि ( ^3 10 = 10^{(10^{10})})—जिसका अर्थ है कि आप इन घातांकों को स्टैक करते हैं। यह सिर्फ तीन शून्य से अधिक है; इसमें एक के बाद 10 अरब शून्य शामिल हैं!

ऐसी संख्या मानव द्वारा लिखी या दृष्टिगत करना असंभव है, और न ही प्रयोगात्मक अनुप्रयोगों में इसका उपयोग करना। वास्तव में, टेट्रेशन संख्याओं को ऐसे क्षेत्रों में स्केल करता है जहाँ उन्हें लिखना भी भौतिक रूप से संभव नहीं होता।

Why tetration numbers are larger than the universe

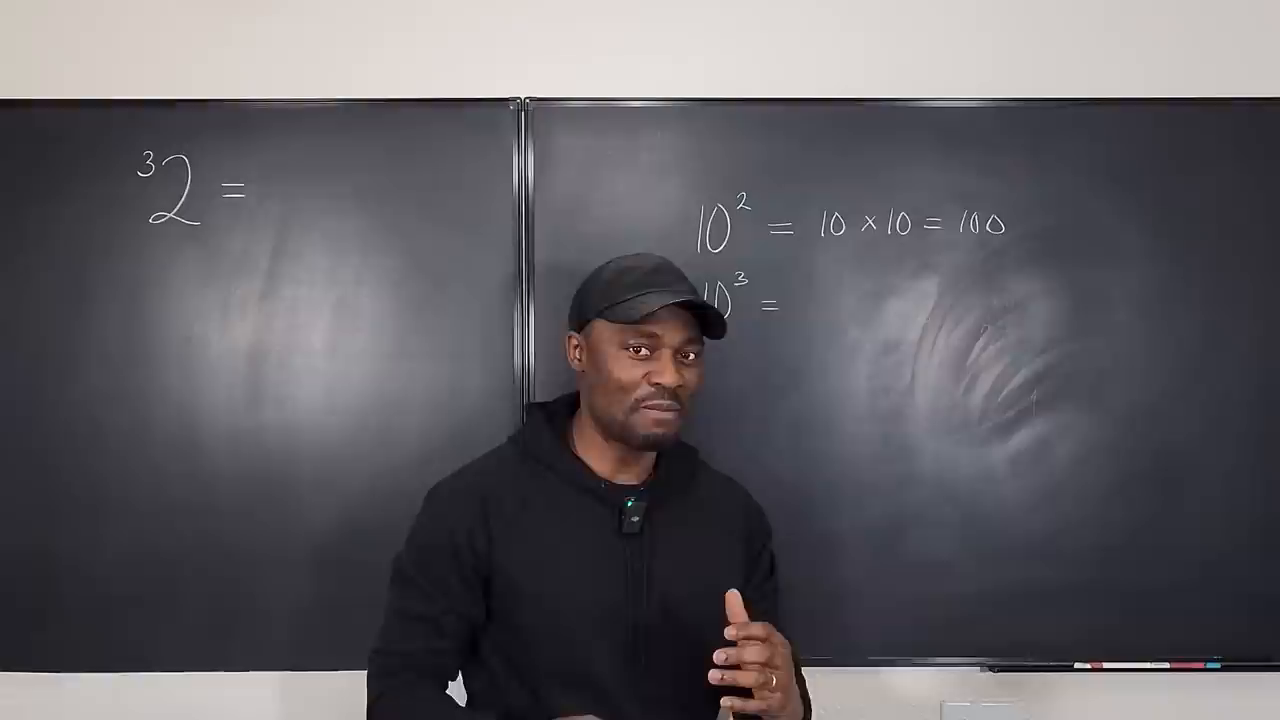
Tetration produces numbers larger than the total atoms in the universe

प्रस्तुतकर्ता समझाते हैं कि (10^{10^{10}}) एक ऐसा संख्या उत्पन्न करता है जो इतनी बड़ी है कि यह कॉस्मिक स्केल्स को पार करती है। टेट्रेशन के साथ एकल गणना दृश्यमान ब्रह्मांड में कुल परमाणुओं की संख्या को भी पार करती है!

यह उदाहरण यह स्पष्ट करता है कि टेट्रेशन दैनिक गणित में क्यों कम उपयोगी है। संख्याएँ इतनी तेजी से बढ़ती हैं कि वे मानव समझ, भंडारण और अनुप्रयोग की सीमाओं को पार कर जाती हैं। उनके सिद्धांतात्मक स्वार्थ के अलावा वे व्यावहारिक परिदृश्यों से भी अज्ञात रहती हैं।

Translating tetration to exponential notation

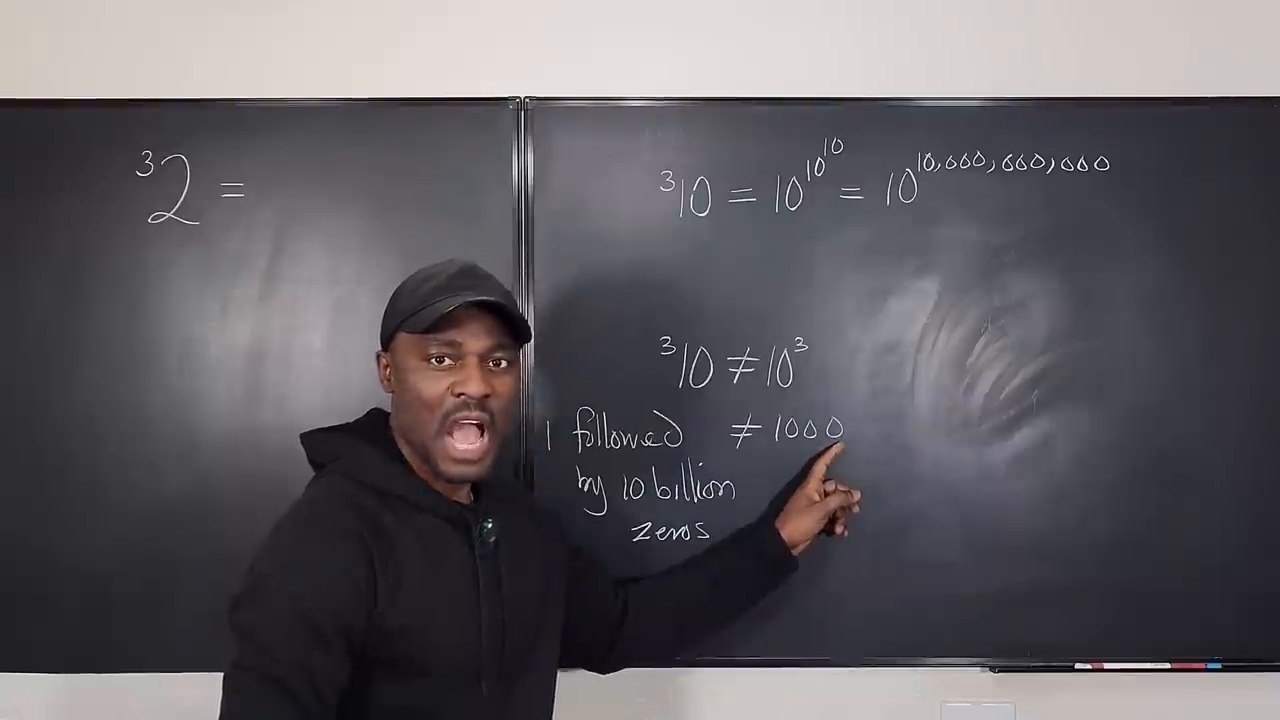
Converting tetration into an expressible exponential format

टेट्रेशन को वापस घातांक में तोड़ने की प्रक्रिया को समझाने के लिए प्रस्तुत किया गया है कि यह क्रिया कैसे कार्य करती है। उदाहरण के लिए:

• ( ^3 10 ) को (10^{10^{10}}) के रूप में लिखा जा सकता है।
• इसका विस्तार करने से इसमें 10 अरब जोड़ना और स्वयं पर पुनरावृत गुणा करना शामिल होगा।

फिर भी, यहाँ एक मुख्य सीख यह है कि टेट्रेशन व्यावहारिक अनुप्रयोगों को पार करता है। यहाँ तक कि इन संख्याओं को गणितीय रूप से व्यक्त करना भी संख्यात्मक रूप से थकाउ है, और उन्हें लागू करना तो और भी कठिन है।

Why tetration isn’t widely taught

प्रस्तुतकर्ता विनोदी ढंग से इस बात का पता लगाते हैं कि टेट्रेशन जैसे सिद्धांतों का अध्ययन व्यापक रूप से क्यों नहीं किया जाता। मुख्य कारणों में शामिल हैं:

• दैनिक संख्याओं के लिए अप्रयुक्तता: वे इतनी तेजी से बढ़ते हैं कि वे संख्यात्मक या वैज्ञानिक गणनाओं के लिए प्रासंगिकता को पार कर जाते हैं।
• शैक्षणिक सीमाएँ: एक निश्चित बिंदु के बाद, ऐसे संख्याओं का व्यवहार उस सीमा से पार हो जाता है जिसे स्कूल सिखाए जाने का लक्ष्य रखते हैं।
• प्रतिनिधित्व में असंभवता: टेट्रेशन द्वारा उत्पन्न शून्यों का एक अंश भी लिखना संभव नहीं है बिना मानव की आयु सीमा को पार किए।

Conclusion: Understanding, not using, tetration

टेट्रेशन एक मन को झकझोरने वाला सिद्धांत है जो संख्याओं को अतिरंजित क्षेत्र में बढ़ाता है। इसके आकर्षक गुणों और गणितीय उत्कृष्टता के बावजूद, इसके वास्तविक जीवन में अनुप्रयोग प्रायः अनुपस्थित हैं। वीडियो का प्रस्तुतकर्ता दर्शकों को इन विशाल संख्याओं के बारे में गंभीरता से सोचने की चुनौती देते हैं और उन्हें अधिक अन्वेषण करने के लिए प्रोत्साहित करते हैं, याद दिलाते हुए: "जिन्हें सीखना बंद कर दिया है, वे जीना बंद कर चुके हैं।"

हालांकि टेट्रेशन आपके दैनिक गणनाओं में शामिल नहीं हो सकता है, यह गणित में मौजूद विशाल विविधता और रचनात्मकता का एक झलक प्रदान करता है—एक ऐसा विषय जो वास्तव में अनंत है, ठीक उसी तरह जैसे संख्याएँ जो टेट्रेशन उत्पन्न करती है।

[Buy the T-shirt with the concept of tetration here: shorturl.at/HNUX1]