Khám Phá Tetration: Những Số Lớn Kỳ Diệu Vượt Qua Toán Học Hằng Ngày

Toán học là một lĩnh vực rộng lớn và đầy những khái niệm thường không được chạm tới ngoài các vòng tròn học thuật. Một trong những khái niệm đó là tetration, một phép toán toán học liên quan đến khai thác lũy thừa lặp lại, tạo ra những con số không thể tưởng tượng nổi. Trong bài viết này, chúng tôi sẽ khám phá tetration, hiểu ý nghĩa của nó (hoặc sự thiếu vắng trong đời sống hàng ngày) và làm rõ cách nó khác với các phép toán toán học truyền thống như cộng, nhân và lũy thừa. Nếu bạn chưa bao giờ thấy một con số như những con số đã được đề cập ở đây—bạn không phải là người duy nhất. Hãy cùng nhau khám phá lĩnh vực thú vị này về những con số lớn.

Giới thiệu về tetration và sự hiếm hoi của nó

Tetration: Bước vào thế giới của những con số khổng lồ

Video bắt đầu bằng việc nói rằng hầu hết mọi người trên trái đất sẽ không bao giờ gặp phải những con số có độ lớn này trong cuộc sống của họ—đừng nói đến việc sử dụng chúng. Tại sao? Bởi vì tetration tạo ra những con số lớn đến mức không thể hiểu nổi. Những con số kết quả từ tetration "lớn hơn những gì bạn có thể tưởng tượng" vì ngay cả khi được biểu diễn với các cơ số nhỏ, quy mô của chúng vượt xa các khái niệm số học thông thường.

Khác với phép cộng hoặc phép nhân, mà chúng ta thường sử dụng trong các công việc hàng ngày, hoặc lũy thừa, thường xuất hiện trong các tính toán khoa học và tài chính, các phép toán tetration leo thang vào quy mô mà có ý nghĩa tối thiểu trong các ứng dụng thực tế.

Tetration là gì?

Tetration, được ký hiệu là ( ^n a ), về cơ bản là một phép toán lũy thừa lặp lại. Để hiểu điều này, chúng ta hãy bắt đầu với một số phép toán cơ bản để so sánh:

Cộng: Cộng lặp lại một số, chẳng hạn như (3 + 3 + 3), cho (9).
Nhân: Cộng lặp lại, chẳng hạn như (3 \times 3 = 9).
Lũy thừa: Nhân lặp lại, chẳng hạn như (3^3 = 27).

Tetration, tuy nhiên, đưa điều này lên một bước xa hơn. Ví dụ, ( ^3 10 ) có nghĩa là (10^{10^{10}})—một con số lớn đến mức không thể biểu diễn bằng các định dạng số học thông thường.

Trong video, người thuyết trình bắt đầu bằng cách chỉ ra một cách đơn giản để hiểu lũy thừa trước khi đi vào tetration.

Giải thích về lũy thừa: Khối xây dựng

Hiểu về lũy thừa như là nền tảng của tetration

Bắt đầu với lũy thừa, người thuyết trình nhấn mạnh sự đơn giản của nó thông qua các ví dụ quen thuộc:

Xem xét (10^2): Điều này tương đương với (10 \times 10 = 100). Số mũ (“2”) chỉ ra số lần bạn nhân cơ số ((10)) với chính nó.
Khi bạn tăng số mũ, số kết quả sẽ tăng theo cấp số nhân. Ví dụ, (10^3 = 1,000), tăng gần 900 so với (10^2).

Hiệu ứng của việc tăng số mũ chỉ một chút được mô tả là "khổng lồ," đặc biệt khi cơ số lớn. Sự tăng trưởng nhanh chóng này là trung tâm để hiểu cách mà các con số xoay vần vượt khỏi tầm kiểm soát trong tetration.

Độ lớn của lũy thừa

Một sự gia tăng trong số mũ, ngay cả với 1, dẫn đến sự tăng trưởng số dứt khoát

Người thuyết trình sử dụng những phép so sánh dễ hiểu để minh họa sự tăng trưởng số có thể trở nên quan trọng đến mức nào:

Hãy tưởng tượng lương hàng tháng của bạn đột nhiên tăng từ $100 lên $11,000—đây là hiệu ứng của việc thêm một chữ số vào số mũ. Khoảng cách giữa những con số như vậy thực sự khổng lồ, đại diện cho hiệu ứng khuếch đại mạnh mẽ của lũy thừa.

Ví dụ:

(10^4 = 10,000), đó là sự tăng 9,000 so với (10^3 = 1,000).
Khi số mũ tăng với một cơ số lớn hợp lý, sự khác biệt giữa các kết quả tích tụ hơn nhiều so với phép cộng hoặc phép nhân.

Giới thiệu về tetration

Đi xa hơn các phép lũy thừa cơ bản, người thuyết trình giới thiệu tetration và sử dụng điều này để làm nổi bật sự tăng trưởng thiên văn của nó so với phép lũy thừa đơn giản.

Hình dung tetration: Sử dụng lũy thừa như một bàn đạp cho khái niệm này

Trong một ví dụ, chúng ta khám phá tetration thứ ba của 10. Được viết là ( ^3 10 ), điều này mở rộng thành (10^{10^{10}}). Đây là phân tích chi tiết:

(10^3 = 1,000), điều này liên quan đến việc nhân (10 \times 10 \times 10).
Bây giờ hãy tưởng tượng rằng ( ^3 10 = 10^{(10^{10})})—có nghĩa là bạn xếp chồng những số mũ này. Điều này vượt xa việc chỉ có ba số không; nó liên quan đến một con số được theo sau bởi 10 tỷ chữ số không!

Một con số như vậy là không thể hiểu nổi cho con người để viết hoặc hình dung, chứ đừng nói đến việc sử dụng trong các ứng dụng thực tế. Hiệu quả, tetration đã nâng quy mô con số lên các lĩnh vực mà ngay cả việc viết chúng ra cũng trở nên không thể.

Tại sao các số tetration lớn hơn vũ trụ

Tetration tạo ra những con số lớn hơn tổng số nguyên tử trong vũ trụ

Người thuyết trình giải thích rằng (10^{10^{10}}) dẫn đến một con số lớn đến mức vượt qua các quy mô vũ trụ. Một phép tính đơn giản với tetration tạo ra một giá trị lớn hơn tổng số nguyên tử trong vũ trụ quan sát được!

Ví dụ này nhấn mạnh lý do tại sao tetration có ít ứng dụng trong toán học hằng ngày. Các con số lớn lên nhanh chóng đến mức vượt qua ranh giới của sự hiểu biết, lưu trữ và ứng dụng của con người. Ngoài sự quan tâm lý thuyết của chúng, chúng vẫn chưa được kết nối với các kịch bản thực tế.

Chuyển đổi tetration sang ký hiệu lũy thừa

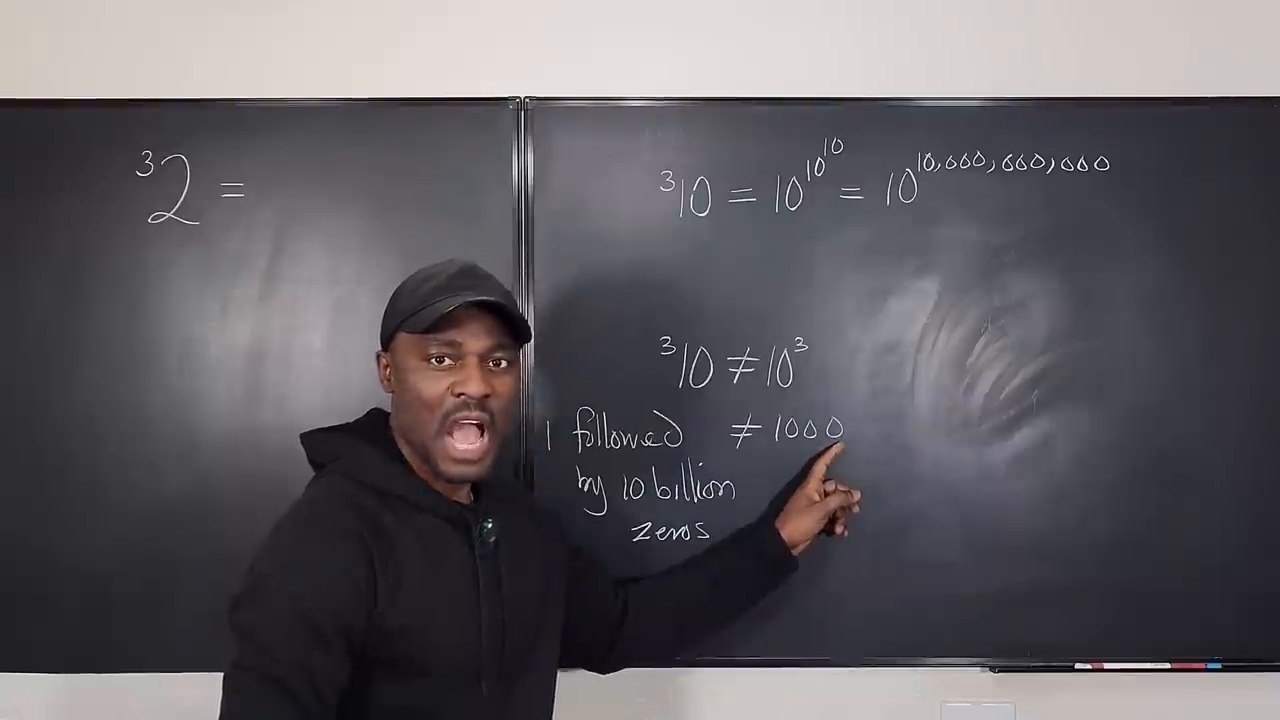
Chuyển đổi tetration thành định dạng lũy thừa có thể diễn đạt

Quá trình phân tích tetration trở lại thành lũy thừa được giới thiệu như một cách để hiểu cách mà phép toán này hoạt động. Ví dụ:

( ^3 10 ) có thể được viết thành (10^{10^{10}}).
Mở rộng điều này sẽ liên quan đến việc xếp chồng 10 tỷ và lặp lại phép nhân trên chính nó.

Tuy nhiên, một điểm chính cần lưu ý ở đây là tetration vượt qua các ứng dụng thực tế. Ngay cả việc diễn đạt những con số này một cách toán học cũng rất tốn sức, chưa nói đến việc áp dụng chúng.

Tại sao tetration không được dạy rộng rãi

Người thuyết trình một cách hài hước đề cập đến lý do tại sao các khái niệm như tetration không được nghiên cứu sâu. Những lý do chính bao gồm:

Tính không thực tế đối với các con số hàng ngày: Chúng phát triển nhanh chóng đến mức thoát khỏi sự liên quan đối với các tính toán số học hoặc khoa học.
Giới hạn giáo dục: Vượt qua một điểm nhất định, hành vi của những con số như vậy vượt quá những gì trường học nhắm đến dạy.
Không thể đại diện: Thực sự không thể viết thậm chí một phần của những chữ số không được tạo ra bởi tetration mà không vượt quá tuổi thọ của con người.

Kết luận: Hiểu, không sử dụng, tetration

Tetration là một khái niệm làm nảy sinh những con số vào các lãnh thổ không thể tưởng tượng nổi. Mặc dù có những tính chất thú vị và vẻ đẹp toán học, nhưng ứng dụng thực tế của nó gần như không tồn tại. Người thuyết trình của video thách thức người xem suy nghĩ một cách phê phán về những con số khổng lồ này và khuyến khích họ khám phá thêm, nhắc nhở chúng ta: “Những ai dừng học hỏi đã dừng sống.”

Mặc dù tetration có thể không tìm thấy đường vào các phép tính hàng ngày của bạn, nhưng nó cung cấp cái nhìn sâu sắc về sự đa dạng và sáng tạo khổng lồ trong toán học—một chủ đề thực sự không có giới hạn, giống như những con số mà tetration tạo ra.

[Mua áo phông với khái niệm tetration ở đây: shorturl.at/HNUX1]