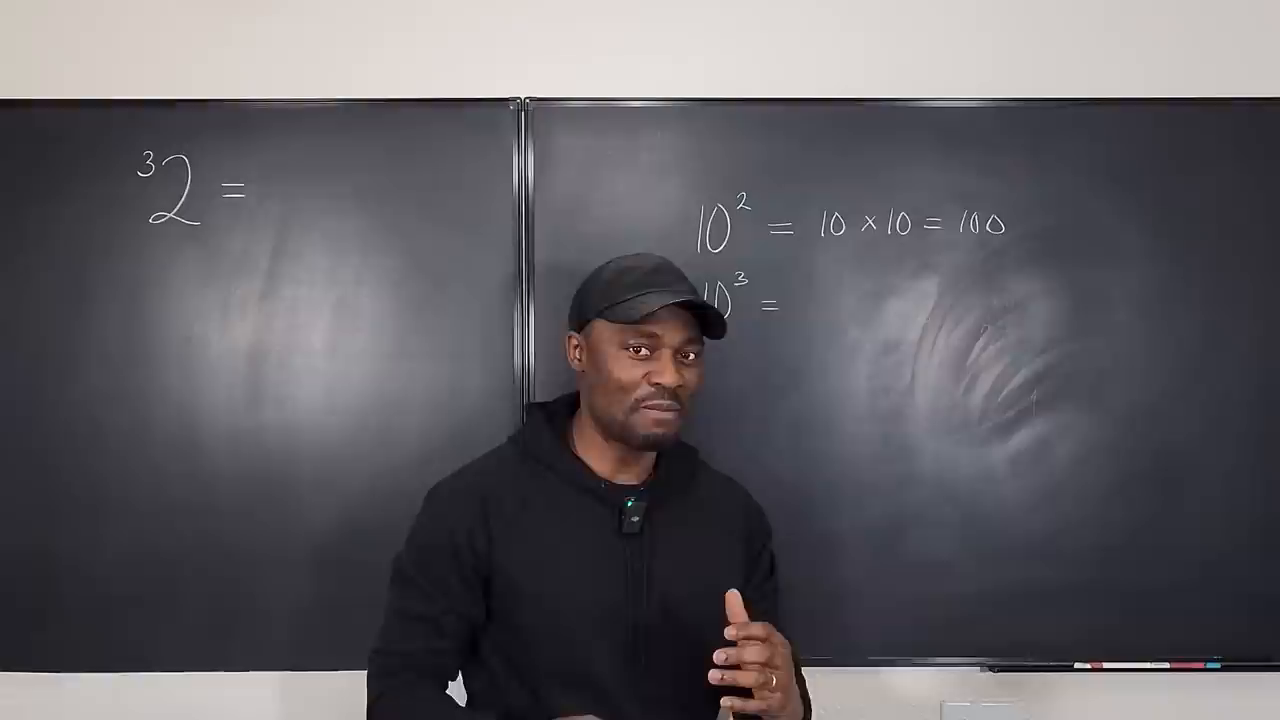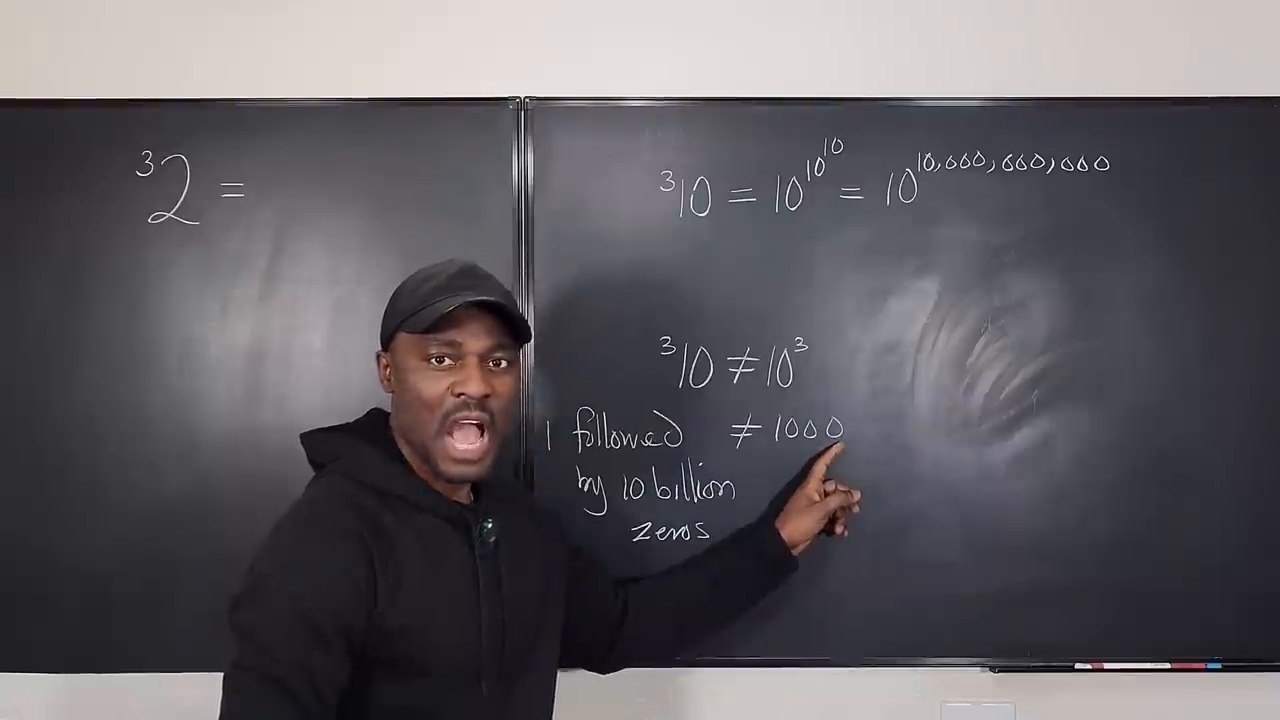探索 t 掉:普通数学之外的巨大数字
数学是广博的,充满了经常在学术圈之外未被触及的概念。一个这样的概念是 t 掉,这是一个涉及重复指数运算的数学操作,创造出难以想象的大数字。在本文中,我们将深入探讨 t 掉,理解其重要性(或在日常生活中的缺乏相关性),并澄清它与传统数学运算(如加法、乘法和指数)的不同之处。如果您从未见过像这里讨论的这些数字——您并不孤单。让我们一起探索这个令人着迷的巨大数字领域。
t 掉简介及其稀有性
视频开始时指出,大多数地球上的人将永远不会在生活中遇到这一数量级的数字——更不用说使用它们了。为什么?因为 t 掉产生的数字是如此巨大,以至于令人难以理解。 由 t 掉结果得出的数字“比你能想象的还要大”,因为即使用小基数表示,其尺度也远远超过典型数字概念。
与我们日常任务中常用的加法或乘法不同,或出现在科学和金融计算中的指数,t 掉操作上升到的规模几乎与实际应用无关。
什么是 t 掉?
t 掉,用符号表示为 ( ^n a ),本质上是一个迭代的指数运算操作。为了理解这一点,让我们先用一些基本运算进行比较:
- 加法:重复加一个数字,例如 (3 + 3 + 3),得到 (9)。
- 乘法:重复加法,例如 (3 \times 3 = 9)。
- 指数:重复乘法,例如 (3^3 = 27)。
t 掉,然而,进一步扩展了这一概念。例如,( ^3 10 ) 代表 (10^{10^{10}})—这是一个如此巨大的数字,以至于在典型数字格式中无法表达。
在视频中,演讲者首先展示了一种简单的了解指数的方法,然后深入探讨 t 掉。
指数解释:构建基石
从 指数 开始,演讲者通过熟悉的例子强调其简单性:
- 考虑 (10^2):这相当于 (10 \times 10 = 100)。指数(“2”)指定你将基数((10))乘以自身的次数。
- 当你增加指数时,结果数字以指数级增长。例如,(10^3 = 1,000),与 (10^2) 相比几乎增加了 900。
即使是稍微增加指数,其影响被描述为 “巨大”, 尤其是当基数较大时。这个快速增长是理解在 t 掉期间数字如何迅速失控的关键。
指数的规模
演讲者使用贴切的类比来说明数字增长的显著程度:
- 想象你的月薪突然从 $100 增加到 $11,000——这就是将单个数字加到指数中的效果。这些数字之间的差距真的是 天文数字,代表了指数的强大放大效应。
例如:
- (10^4 = 10,000),与 (10^3 = 1,000) 相比增加了 9,000。
- 当指数在基数相对较大的情况下增加时,结果之间的差距比加法或乘法更严重地累积。
介绍 t 掉
超越基本的指数,演讲者介绍了 t 掉,并借此突出其与简单指数相比的天文增长。
在一个例子中,我们探讨 10 的第三个 t 掉。写作 ( ^3 10 ),扩展为 (10^{10^{10}})。下面是分解:
- (10^3 = 1,000),涉及到 (10 \times 10 \times 10) 的乘法。
- 现在想象 ( ^3 10 = 10^{(10^{10})})—意思是你堆叠这些指数。这远远超过仅仅三个零;它涉及到一个后面跟着 10 亿个零 的数字!
这样一个数字对于人类来说是 难以理解 的,既无法用笔写下或可视化,更不用说在实际应用中使用。有效地说,t 掉将数字放大到即使书写都变得不可能的领域。
为什么 t 掉数字比宇宙还要大
演讲者解释说,(10^{10^{10}}) 得出的数字是如此之大,以至于超过了 宇宙尺度。通过 t 掉的单一计算产生的值大于 可观察宇宙中原子的总数!
这个例子强调了为什么 t 掉在日常数学中用处不大。数字增长如此迅速,超出了人类理解、存储和应用的范围。超越它们的理论兴趣,它们仍然与实际场景无关。
将 t 掉转换为指数符号
介绍将 t 掉分解回指数的过程作为了解其功能的方式。例如:
- ( ^3 10 ) 可写作 (10^{10^{10}})。
- 展开这个将涉及堆叠 10 亿 并反复进行自乘的操作。
然而,这里一个关键的收获是 t 掉绕过了现实应用。 即使在数学上表达这些数字也极其耗尽计算能力,更不用说应用它们。
为什么 t 掉没有被广泛教授
演讲者幽默地讨论了为什么像 t 掉这样的概念没有得到广泛研究。主要原因包括:
- 对日常数字的不实用性:它们增长如此迅速,以至于超出了数值或科学计算的相关性。
- 教育限制:超出某一点后,这些数字的行为超过了学校希望教授的内容。
- 不可表示性:即使是写出 t 掉所产生的零的一小部分也是字面上不可能,在没有超过人类寿命的情况下。
结论:理解而非使用 t 掉
t 掉是一个令人震撼的概念,将数字放大到不可思议的领域。尽管它具有迷人的特性和数学优雅,但其实际应用几乎不存在。视频的演讲者挑战观众批判性思考这些巨大数字,并鼓励他们进行更多探索,提醒我们:“那些停止学习的人已经停止生活。”
虽然 t 掉可能不会进入您的日常计算,但它提供了对数学内在巨大多样性和创造力的洞察——这是一个真正无边无际的主题,正如 t 掉产生的数字一样。
[在这里购买有关 t 掉概念的 T 恤:shorturl.at/HNUX1]